算法数据结构散列 hash

数据结构-散列表(hash table)

4FGR2024-12-012024-12-03

数据结构-散列表(hash table)

参考资料：数据结构与算法分析 –Mark Allen Weiss

一、基本介绍

散列(hashing) ：一种以常数平均时间执行插入、删除和查找的技术，但对元素间进行排序的操作不被支持，例如寻找最大值和最小值。

散列表（hash table）: 一个含有关键字的具有固定大小的数组，通过关键字查找对应值，只需要O(1)的时间复杂度。

散列函数：将每个关键字映射到从0到size-1这个范围中的某个数，并且放到适当的单元。这个映射就叫做散列函数。

二、散列函数

关键字为整数的设置方法:

如果输入的关键字是整数，则一般合理的方法就是直接返回关键字% 表长, 最好保证表长为素数（质数），以避免某些特殊情况，例如表长为10，而关键字均以0为个位的情况。

关键字为字符串的设置方法:

通常，关键字是字符串，在这种情形下，散列函数需要仔细选择。

用ASCII码直接相加并取余并不合适, 表长很大，就不能均匀地很好地分配关键字。

代码如下

int Hash(const char *key, int len)

{

	unsigned int hash = 0; //显然，hash值不为负

	while( *key != '\0') {hash += *key; key++;}

	return hash % len;

}

而另一个散列如代码所示, 当key长度为3时：

int Hash( const char *key, int len)
{
    return (key[0] + 27 * key[1]+ 27*27 key[2]) % len;
}

27表示英文字母加一个空格的个数，如果key是随机的，那么就会得到一个合理分配，但英文不是随机的, 这导致我们会造成很大的空间浪费，特别是表长足够大时。

下面列出一个较好的方法,它计算：

$\sum_{i = 0}^{k e y s i z e - 1} k e y [k e y s i z e - i - 1] \times 32^{i}$

程序根据Horner法则计算一个(32的)多项式函数,之所以不用27，是因为32可以通过”<<”右移五位获得

Horner法则，例如 res = n₁ + 27n₂ + 27²n₃可转换为 res = ( (k₃) *27+k₂)* 27 + n₁

代码如下：

int Hash(const char *key, int len)
{
    unsigned int hash = 0; //显然hash值为0,数组下标是为正的
    while(*key != '\0')
    {
    	hash = (hash<<5) + *key;
        key++;
    }
    return hash % len;
    
}

剩下解决的就是当插入元素对应的散列值(hash)已经存在，如何消除这个冲突的问题，我们讨论最简单的两种:

分离链接法 和 开放定址法

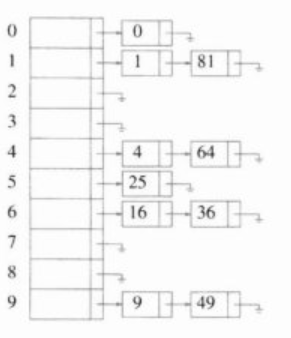
三、分离链接法

将散列到同一个值的所有元素保留在一个表中。为方便起见，这些表都有表头，如果空间很紧，更可取的方法是避免使用这些表头。（表长不用素数是为了简单起见，这里表长为10）

//结构体的定义
struct ListNode{
    E data; //元素类型为E
    ListNode *next;
};
typedef struct ListNode ListNode,*List;
typedef struct HashTbl{
    int size;
    List *lists;
}*HashTable;

为简洁需要，以下代码并未有健壮性检查，自己实现时记得加上()。

初始化：它用到与栈的数组实现中相同的想法。设置表的大小为一个素数，指定List的一个指针数组,如果要有表头，就必须给每个表分配一个表头并且设置next为NULL；

HashTable InitalizeTable(int size){
	HashTable H;
	int i;
    H = (HashTable)malloc(sizeof(struct HashTbl));
    H->size = size;
    /* 为确保size是质数，可实现NextPrime函数
    H->size = NextPrime(size);
    */
    H->lists = (List *)malloc(sizeof(List)*H->size);
    for(i = 0; i<H->size; i++){
        H->lists[i] = (List)malloc(sizeof(ListNode));
        H->lists[i]->next = NULL;
    }
    return H;
}

查找：我们使用散列元素来确定究竟考察哪个表，此时通常采用遍历的方式,返回被查找项所在位置

如果data类型是字符串，则比较和赋值相应地用strcmp和strcpy进行

ListNode* Find(E key, HashTable H){  //返回关键字对应的指针
    ListNode *p,*l;
    l = (List)H->lists[Hash(key, H->size)];  //找到对应的表
    p = l->next;
    while(p!=NULL && p->data != key){
        p = p->next;
    }
    return p;
}

插入：查找元素是否已经处在合适的位置(如果要插入重复元，那么通常要留出一个额外的域，这个域党重复出现时自增1)，根据容易度，新元素或者插入表的前端，或者后端。有时将新元素插入到表的前端不仅方便，而且还因为新进插入的元素最有可能优先被访问。

void Insert(E key, HashTable H){
	ListNode *pos,*p;
    List l;
    
    pos = Find(key, H);
    if(pos == NULL){  //key不在散列中,可以插入
        p = (ListNode *)malloc(sizeof(ListNode));
        l = H->lists[Hash(key, H->size)];
        p->next = l->next;  //此处采用前插法
        p->data = key;
        l->next = p;
    }
}

四、开放定址法

分离链接法的缺点是需要指针，由于给新单元分配地址需要时间，因此这就导致算法的速度多少有些减慢。开放定址散列法（open addressing hashing）是另外一种用链表解决冲突的方法, 如果有冲突发生，就尝试找到另外空的单元。更一般地，单元 h₀(X), h₁((X), ···,相继试选，其中h_i((X)=(Hash(X)+F(i)) % size,且F(0) = 0。函数F是冲突解决方法。因为所有的数据都要置入表内，所以该算法所需要的表要比分离链接法的表要大，一般说来，装填因子应该低于0.5。现在我们就来考察三个通常的冲突解决方法。

1.线性探测法

在该方法中，函数F为i的线性函数，常用F(i)=i。这相当于逐个探测每个单元(必要时可以绕回)以查找出一个空单元。只要表足够大，总能找到一个自由单元，但较为消耗时间。另外，即便表相对较空，这样占据的单元也会开始形成一些区块，其结果称为一次聚集（primary clustering）。于是，散列到区块中的任何关键字都需要多次试选，才能被添加到相应的区块中。

2.平方探测法

平方探测法是一种消除线性探测中一次聚集问题的冲突解决方法，是冲突函数为二次函数的方法，常用F(i)= i²。例如，对于49,89,18,58而言,当要放89时，其位置与49发生冲突，其下一个位置为下一个单元，而当要放58时，其后相邻的单元经探测得知发生了另外的冲突。其下一个位置在距离位置8为 2²=4 远处，也就是位置2处。

对于线性探测，让元素填充满散列表并不好，而对于本方法而言情况甚至更糟。如果使用平方探测，且表的大小是素数，那么当表至少有一半是空的时候，总能够插入一个新的元素。

在开放定址散列表中，删除操作需要懒惰删除，虽然这种情况并不存在真正意义上的懒惰。

实现开放定址散列:

typedef unsigned int Index;
typedef int E;
enum KindOfEntry{Legitimate, Empty, Deleted};

typedef struct HashEntry{
    E data;
    enum KindOfEntry info;
}Cell;

typedef struct HashTbl{
    int size;
    Cell *cells;
}*HashTable;

初始化:由分配空间和其后每个单元的info域设置成Empty组成

HashTable InitializeTable(int size){
    HashTable H;
    int i;
    H = (HashTable)malloc(sizeof(struct HashTbl));
    H->size = size;
    H->cells = (Cell *)malloc(sizeof(Cell)*H->size);
    for(i = 0; i<H->size; i++){
        H->cells[i].info = Empty;
    }
    return H;
}

查找：找到返回key的位置，否则返回最后的单元，以方便插入。查找是否失败，通过枚举值便知晓。

Index Find(E key, HashTable H){
    Index CurrentPos;
    int CollisionNum;

    CollisionNum = 0;
    CurrentPos = Hash(key, H->size);
    while(H->cells[CurrentPos].info != Empty && H->cells[CurrentPos].data != key){
        CurrentPos += 2*++CollisionNum - 1;  //平方探测法
        if(CurrentPos >= H->size){
            CurrentPos -= H->size;
        }
    }
    return CurrentPos;
}

插入:将插入的元素放在Find所指出的地方。

void Insert(E key, HashTable H){
    Index Pos;
    Pos = Find(key, H);
    if(H->cells[Pos].info != Legitimate){
        H->cells[Pos].info = Legitimate;
        H->cells[Pos].data = key;
    }
}

虽然平方探测法排除了一次聚集，但是散列到同一位置上的那些元素将探测相同的备选单元，这叫做二次聚集(secondary clustering)。这是理论上的一个小缺憾，模拟结果指出，它一般要引起另外的少于一半的探测。下面的技术将会排除这个缺憾。

3.双散列

我们考察的最后一个冲突解决方法叫做双散列(double hashing)。对于双散列，一种流行的选择是F(i)=i*hash₂((X)。显然，hash2选择得不好将会是灾难性的，函数一定不要算得0值。另外，保证所有单元都能被探测到也是很重要的，诸如 hash₂((X)=R-(X % R) 这样的函数将起到良好的作用。其中R为小于size的素数。如果表的大小不是素数，那么备选单元就有可能提前用完。但由于平方探测不需要使用第二个散列函数，从而在实践中可能更简单并且更快。

五、再散列

对于使用平方探测的开发定址散列法，如果表中元素太满，那么操作的运行时间将开始消耗过长，且插入操作可能失败。此时，一种解决方法是建立另外一个大约两倍大的表（而且使用一个相关的新散列函数），扫描整个原始散列表，计算每个元素的新散列值并将其插入到新表中。整个操作就叫做再散列(rehashing)。

显然这是一种较为昂贵的操作，运行时间为O(n), 但由于不是经常发生，因此实际效果还行。特别是，在最后的再散列之前必然已经存在N/2次的Insert, 当然添加到每个插入上的花费基本上是一个常数开销。

推荐再散列的一种实现方法：途中(middle-of-the-road)策略

当表到达某一个装填因子时进行再散列。由于随着装填因子的增加，表的性能的确有下降，因此，以好的截止手段实现，可能是最好的策略。

再散列使我们再不用担心表的大小，这很重要，因为在复杂的程序中散列表不能够做到任意大。

对开放定址散列表的再散列：

HashTable Rehash( HashTable H){
    int i,OldSize;
    Cell *OldCells;

    OldCells = H->cells;
    OldSize = H->size;
    
    H = InitializeTable(2* OldSize);

    for(i = 0; i < OldSize; i++){
        if(OldCells[i].info == Legitimate)
            Insert( OldCells[i].data, H);
    }
    free(OldCells);
    return H;
}

感谢观看！

数据结构-散列表(hash table)

一、基本介绍

二、散列函数

三、 分离链接法

四、开放定址法

1.线性探测法

2.平方探测法

3.双散列

五、再散列

4FGR

三、分离链接法