梦境巡查-第三十六次CCF认证(CSP)第二道题个人题解

题目链接：TUOJ（需有账号）

题目背景

传说每当月光遍布西西艾弗岛，总有一道身影默默守护着居民们的美梦。

题目描述

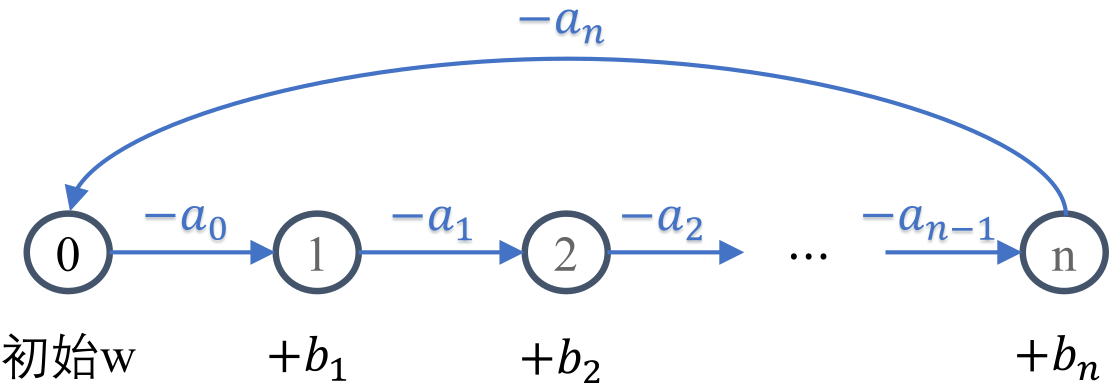
梦境中的西西艾弗岛由 n+1n+1 个区域组成。梦境巡查员顿顿每天都会从梦之源（00 号区域）出发，顺次巡查 1,2,⋯,n1,2,⋯,n 号区域，最后从 nn 号区域返回梦之源。

在梦境梭需要消耗美梦能量：

  • 从梦之源出发时，顿顿会携带若干初始能量；
  • 从第 ii 号区域前往下一区域（0≤i≤n0≤i≤n）需要消耗 aia**i 单位能量，因此从第 ii 号区域出发时，顿顿剩余的美梦能量需要大于或等于 aia**i 单位；
  • 顺利到达第 ii 号区域（1≤i≤n1≤i≤n）后，顿顿可以从当地居民的美梦中汲取 bib**i 单位能量作为补给。

假设顿顿初始携带 ww 单位美梦能量，那么首先需要保证 w≥a0w≥a0，这样顿顿便可消耗 a0a0 能量穿梭到 11 号区域、进而获得 b1b1 单位能量补给。巡查 11 号区域后，顿顿剩余能量为 w−a0+b1w−a0+b1，如果该数值大于或等于 a1a1，顿顿便可继续前往 22 号区域。依此类推，直至最后消耗 ana**n 单位能量从 nn 号区域返回梦之源，便算是顺利完成整个巡查。西西艾弗岛，又迎来安宁的一夜，可喜可贺！

作为一个成熟的梦境巡查员，顿顿已经知晓初始需要携带多少能量可以保证顺利完成巡查。但在一些意外状况下，比如学生们受期末季的困扰而无法安眠，顿顿可能在某些区域无法采集足够的美梦能量。此时，便需要增加初始携带量以备万全。

具体来说，考虑一个简单的情况：在 11 到 nn 号区域中，有且仅有一个区域发生意外，顿顿无法从该区域获得能量补给。 如果第 ii 号区域（1≤i≤n1≤i≤n）发生意外（即 bib**i 变为 00），则此时为顺利完成巡查，顿顿从梦之源出发所携带的最少初始能量记作 w(i)w(i)。

试帮助顿顿计算 w(1),w(2),⋯,w(n)w(1),w(2),⋯,w(n) 的值。

为了简便的需要,我们设置所有数组长度为n+1，数组下标直接与节点对应。

结果为

w[i] = dp1[i] + max(0,dp2[i] - remain[i]);

当然 w[i] = max(dp1[i], dp1[i] + dp2[i] - remain[i]) 也是可以的(下面同理)

我的设置如下:

dp1[i]是到达第i个节点所需要的最小能量

dp2[i]是从第i个节点开始顺利完成任务所需要的最小能量

remain[i]是到达第i个节点前所剩余的能量(当到达方式最优时)

其中dp1的动态转移方程为

dp1[i+1] = dp1[i] + max(0, a[i] - remain[i+1])

dp2的动态转移方程为

dp2[i] = a[i] + max(0, dp2[i+1] - b[i+1])

更新remain:

remain[i+1] = max(0,remain[i+1] - a[i])

(用if语句也行)

我的思路是，既然我们要求当第i节点故障时(即无法获取b[i]能量)，顺利完成任务所需要的最少能量，显然是到达这个节点所需要的最少能量，加上从这个节点到最终节点最后回到起始节点所需要的最少能量。由于到达这个节点时，补给所获取的能量还有剩余，所以可以补充后一段的路程，当然这是不可能直接相减的（后一段最少能量不可能为负数），因此一共是max(0, dp2[i] - remain[i]), 总体就是dp1[i] + max(0, dp2[i] - remain[i])。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

#include<iostream>
#include<cmath>
using namespace std;

int main(){
    ios::sync_with_stdio(0); //取消c++与stdio的同步，使得cin和cout变快
    cin.tie(0);
    int n;
    cin >> n;
    //若下标为i,a[i]表示从第i节点到第i+1节点所需的能量
    //a[n]表示从第n节点回到第0节点所需的能量
    int a[n+1]; 
    //b[i]表示第i节点可补给的能量，b[0]无用
    int b[n+1];
    int dp1[n+1];
    int dp2[n+1];
    int remain[n+1];
    int w[n+1]; //存储结果
    remain[1] = 0; //显然一开始补给点的能量为0
    for(int i=0; i<=n; i++) cin >> a[i];
    dp1[1] = a[0];
    for(int i=1; i<n; i++){
        cin >> b[i];
        remain[i+1] = remain[i]+b[i];
        dp1[i+1] = dp1[i] + max(0, a[i] - remain[i+1]); //获取dp1
		remain[i+1] = max(0,remain[i+1] - a[i]); //更新remain
    }
    cin >> b[n]; //防止dp1、remain数组溢出，单独放置
    dp2[n] = a[n]; //显然从第n节点回到第1节点所需能量为a[n]
    for(int i=n-1; i>0; i--){
        dp2[i] = a[i] + max(0, dp2[i+1] - b[i+1]) ;  //获取dp2
        w[i] = max(dp1[i], dp1[i] + dp2[i] - remain[i]); //得到w[i]
    }
    w[n] = max(dp1[n], dp1[n]+ dp2[n] - remain[n]);
    
    for(int i=1; i<=n; i++) cout << w[i] << ' '; //输出结果

    return 0;
}